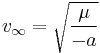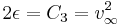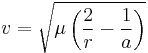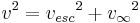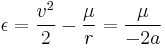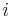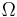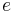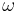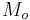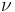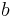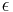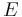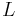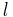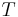Hyperbolic trajectory
In astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with the eccentricity greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body. Similarly to parabolic trajectory all hyperbolic trajectories are also escape trajectories. The specific energy of a hyperbolic trajectory orbit is positive. The shape of a hyperbolic trajectory is a hyperbola.
Contents |
Hyperbolic excess velocity
Under standard assumptions the body traveling along hyperbolic trajectory will attain in infinity an orbital velocity called hyperbolic excess velocity (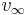 ) that can be computed as:
) that can be computed as:
where:
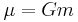 is standard gravitational parameter,
is standard gravitational parameter,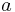 is the negative semi-major axis of orbit's hyperbola.
is the negative semi-major axis of orbit's hyperbola.
The hyperbolic excess velocity is related to the specific orbital energy or characteristic energy by
Velocity
Under standard assumptions the orbital velocity (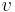 ) of a body traveling along hyperbolic trajectory can be computed as (Vallado):
) of a body traveling along hyperbolic trajectory can be computed as (Vallado):
where:
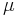 is standard gravitational parameter,
is standard gravitational parameter,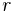 is radial distance of orbiting body from central body,
is radial distance of orbiting body from central body,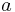 is the negative semi-major axis.
is the negative semi-major axis.
Under standard assumptions, at any position in the orbit the following relation holds for orbital velocity (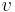 ), local escape velocity(
), local escape velocity(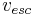 ) and hyperbolic excess velocity (
) and hyperbolic excess velocity (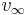 ):
):
Note that this means that a relatively small extra delta-v above that needed to accelerate to the escape speed, results in a relatively large speed at infinity.
Angle between approach and departure
Let the angle between approach and departure (between asymptotes) be 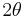 .
.
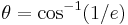 and
and 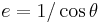
where:
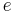 is the orbital eccentricity, which is greater than 1 for hyperbolic trajectories.
is the orbital eccentricity, which is greater than 1 for hyperbolic trajectories.
Distance of closest approach
The distance of closest approach, also called the periapse distance and the focal distance, is given by 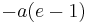
Energy
Under standard assumptions, specific orbital energy (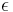 ) of a hyperbolic trajectory is greater than zero and the orbital energy conservation equation for this kind of trajectory takes form:
) of a hyperbolic trajectory is greater than zero and the orbital energy conservation equation for this kind of trajectory takes form:
where:
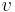 is orbital velocity of orbiting body,
is orbital velocity of orbiting body,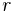 is radial distance of orbiting body from central body,
is radial distance of orbiting body from central body,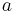 is the negative semi-major axis,
is the negative semi-major axis,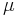 is standard gravitational parameter.
is standard gravitational parameter.
Radial hyperbolic trajectory
A radial hyperbolic trajectory is a non-periodic trajectory on a straight line where the relative speed of the two objects always exceeds the escape velocity. There are two cases: the bodies move away from each other or towards each other. This is a hyperbolic orbit with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1 this is not a parabolic orbit.
See also
References
- Vallado, David A. (2007). Fundamentals of Astrodynamics and Applications, Third Edition. Hawthorne, CA.: Hawthorne Press. ISBN 978-1-881883-14-2.
External links
- http://homepage.mac.com/sjbradshaw/msc/traject.html
- http://www.go.ednet.ns.ca/~larry/orbits/ellipse.html